Statistiques - probabilités - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques - probabilités - Cours Première S
Statistiques - probabilités - Cours Première S
Répétition d'expériences identiques et indépendantes
Il est possible d'obtenir une nouvelle expérience aléatoire en répétant plusieurs fois (2, 3, 4... n fois) la même expérience aléatoire. On s'intéresse ici uniquement au cas où les expériences répétées sont indépendantes les unes des autres, c'est à dire qu'après une l'expérience on retrouve les même condition pour la reproduire avec le même univers et les mêmes lois de probabilité.
Exemples:
- tirer à pile ou face à la même pièce
- Relancer plusieurs fois les mêmes dés
- Effectuer un tirage de boules colorées ou numérotées en reposant à chaque fois les boules
- Effectuer un tirage de jeton en reposant à chaque fois les jetons
Nombre d'issues possibles après répétition d'une expérience
Si l'on repète une expérience aléatoire disposant de deux issue possible:
- si on la réalise une deuxième fois chaque issue de la première expérience peut être associée à deux issues de la seconde soit un total de 2 x 2 = 4 (22) issues possibles
- si on la réalise une troisièmes fois chaque combinaison d'issues obtenue après la seconde expérience peut être associée à deux issues de la troisième soit un total de 4 x 2 = 8 (23) issues possibles.
De même en répétant 4 fois on aurait 8 x 2 = 16 (24) issues, en répétant 5 fois, 16 x 2 = 32 (25)issues etc. on remarque qu'à
D'une manière générale si une expérience aléatoire possède deux issues en la répétant "n" fois on obtient une expérience dont l'univers est composé de 2n issues.
De même si une expérience aléatoire possède trois issues en la répétant "n" fois on obtient une expérience dont l'univers est composé de 3n issues.
Si une expérience aléatoire possède "a" issues en la répétant "n" fois on obtient une expérience dont l'univers est composé de an issues.
Répétition d'expériences et loi de probabilité
Si une variable aléatoire est munie d'une loi de probabilité p alors on admet que qu'en répétant l'expérience "n" fois on obtient une nouvelle issue dont la probabilité est le produit des probabilités de chaque issue intermédiaire.
Exemple
Si l'on répète trois fois de suite un lancer de dé (dé équilibré avec équiprobabilité pour les 6 face)
Alors la probabilité d'obtenir 3 fois de suite le chiffre 6 est de:
p = 1 x 1 x 1
6 6 6
p = 1
216
La probabilité d'obtenir deux fois de suite un nombre paire puis le nombre 1 est de:
p = 1 x 1 x 1
2 2 6
p = 1
24
Arbre pondéré
Il représente les différentes successions possibles d'issues lorsqu'une expérience est répétée et surtout chaque branche comporte la probabilité qui est associée à chaque issue intermédiaire. Pour connaître la probabilité d'une succession d'issues données il suffit de multiplier les probabilités que comporte son embranchement. L'arbre pondérée est surtout utile lorsqu'il n'y a pas équiprobabilité.
Exemple
Un dé à quatre face n'est pas équilibré, les probabilités sont : 0,1 pour la face "1", 0,2 pour la face "2", 0,3 pour la face "3" et 0,4 pour la face "4". Si on lance 3 fois de suite ce dé, voici l'arbre pondéré de cette expérience:
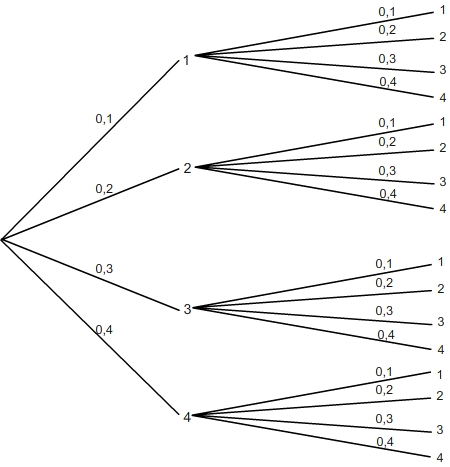
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
